Полезный обзор-лекция по методам статистического описания систем типа скоплеия частиц, связанных взаимным тяготением. Приводятся формулы и для случая расширяющегося пространства.

Галактики приобретают угловой момент за счет приливных воздействий в процессе формирования крупномасштабной структуры. Разумеется, параметры вращения оказывают скоррелированы с другими параметрами галактик и окружающих их структур. Все это так или иначе может проявляться в наблюдениях (в частности, в данных по линзированию). Всему этому и посвящен данный обзор. Написано отнюдь не просто.

Авторы численно исследуют динамическую устойчивость Солнечной системы на больших временах (миллиарды лет). Никакой неустойчивости не найдено (замечу, что исследовать времена более, скажем, пяти миллиардов лет несколько бессмысленно, просто потому, что Солнце эволюционирует). Однако это еще не конец истории. Несколько лет назад Жак Ласкар показал, что планетные орбиты все-таки могут быть неустойчивы (или, если угодно, что обычные методы расчета упускают некоторые возможности развития событий). Поскольку система имеет характеристики хаотической системы, то слабые возмущения могут приводить к большим последствиям (эффект бабочки). Ласкар "руками" вносил слабые возмущения в земную орбиту (Земля смещалась на 150 метров в ту или иную сторону), а затем отбирал сценарии развития событий, в которых эксцентриситет Меркурия возрастал. После шага интегрирования в полмиллиарда лет в систему снова вносились слабые возмущения, и снова отбирались сценарии, где орбита Меркурия все больше вытягивалась. В итоге за 6 миллиардов лет эксцентриситет Меркурия вырос до 0.5. Т.е., есть маленькая вероятность того, что орбиты все-таки будут сильно другими спустя несколько миллиардов лет (для Меркурия Ласкар получил оценку вероятности того, что эксцентриситет вырастет до 0.6 за 5 миллиардов лет, порядка 1 процента).

Авторы применили ласкаровскую технику и показали, что орбиты планет земной группы могут оказываться неустойчивыми на временах порядка миллиарда лет. А вот в мире гигантов все спокойно. Авторы не учитывали эффекты ОТО (Ласкар учитывал). Они обсуждают, насколько это важно в данной задаче.

Замечательный обзор по свойствам звезд в плотных скоплениях. Все эти данные необходимы для задания начальных условий при моделировании динамики скоплений - отсюда и вторая часть заголовка.

Галактики приобретают угловой момент за счет приливных воздействий в процессе формирования крупномасштабной структуры. Разумеется, параметры вращения оказывают скоррелированы с другими параметрами галактик и окружающих их структур. Все это так или иначе может проявляться в наблюдениях (в частности, в данных по линзированию). Всему этому и посвящен данный обзор. Написано отнюдь не просто.

Собственно, статью читателям придется скачивать с сайта автора.

Большой текст, представляющий собой лекции по "отдельным главам Галактической динамики".

Я пропустил эту статью, читая astro-ph, но, к счастью, она появилась в новостях. Работа в самом деле важная и интересная.

В начале об авторах, чтобы не было сомнений. Точнее о первом авторе. По сути, это человек, открывший аномалию Пионеров. Он руководил небесно-механическими расчетами в ряде проектов NASA, например, Galileo. Так что вопрос о компетенции не возникает.

Далее. Авторы описывают интересный наблюдательный эффект. Связан он с тем, что при гравитационных маневрах, призванных увеличить (в случае полетов к внешним планетами т.п.) или уменьшить (в случае полета к внутренним планетам и другим телам, для достижения которых надо "притормозить") кинетическую энергию аппарата. Сам эффект хорошо известен, он использовался для разгона Пионеров 10 и 11 и Вояджеров, Galileo и других аппаратов. Однако, не все так просто. Конечно, мы значем, что спутники летят куда на до и т.п. Тем не менее, есть очень маленький, но интересный эффект. При пролете планеты аппараты получают небольшую дополнительную энергии в сравнении с расчетной. Последнее замечание чрезвычайно важно. Не надо сразу кидаться делать выводы о том, что ньютоновская гравитация даже близко не верна, и что обнаруженный эффект потрясает все основы. Все-таки, вывод состоит лишь в том, что модель, в рамках которой проводятся расчеты, что-то не учитывает.

Существенно, что эффект есть даже для манервов аппаратов около Земли, причем даже в системе координат, связанной с Землей!

Авторы видят возможную связь эффекта с аномалией в движении Пионеров (напомню, что речь идет о наличии дополнительного ускорения, направленного примерно к Солнцу). Дело в том, что аномалия в движении Пионера-11 появилась после гравитационного маневра около Сатурна.

Повторюсь, что эффект достаточно мал, и вероятно связан с недоучетом чего-то в модели. Т.е. говорить о "потрясании священных коров" рано. Тем не менее видно, что даже в хорошо известных областях (а небесная механика к ним безусловно относится) можно обнаруживать очень интересные эффекты!

Добавлю, что данные о форме гало важны, как это не странно, и для физики элементарных частиц. Дело в том, что ряд авторов пытается объяснить избыток гамма-лучей, наблюдавшийся прибором EGRET, как излучение темной материи в гало нашей галактики. Излучение возникает благодаря распаду частиц темной материи. Новые данные о форме гало должны помочь уточнить модели гамма-излучения. Т.о., возможно, можно будет получить данные о суперсимметрии не из ускорительных экспериментов, а из астрофизических данных.

Хорошее описание динамического трения в звездных системах. Непонятно, почему авторы положили статью в эту часть Архива, а не в astro-ph.

Напомню, что явление динамического трения характерной для систем многих тел. Скажем звезда, двигаясь среди других звезд, будет испытывать силу, направленную против движения. Происхождение силы чисто гравитационное. Связано оно с тем, что сама звезда создает своей гравитацией сзади себя сгущение. Похожее явление будет возникать при движении любой тяжелой частицы в сжимаемой среде. Впервые данный феномен был рассмотрен Чандрасекаром. Полагаю, что статья будет интересна многим. Ее можно и полезно разбирать в качестве примера на семинарах по механике или даже с разумными девятиклассниками.

Обширная энциклопедическая статья, посвященная методу многих тел в гравитации.

Все знают, что уже задача трех тел в общем виде не имеет полного аналитического решения. Однако в астрономии сплошь и рядом встречаются ситуации взаимодействия множества объектов. Для решения таких задач были разработаны как численные, так и приближенные аналитические методы. Обо всем этом - в статье.

Автор исследовал устойчивость маломассивных звездных скоплений вокруг тяжелых центральных объектов. Примером таких систем является звездное скопление вокруг центральной черной дыры нашей Галактики и кометное облако Оорта вокруг Солнца.

При отсутствии самогравитации (т.е. когда движение звезд определяется только центральным объектом) устойчивость таких систем зависит от функции их распределения F по угловому моменту J: если при фиксированной энергии

Тесные пролеты и лобовые столкновения звезд в плотных скоплениях (шаровых и скоплениях вблизи центров галактик) приводят к образованию очень массивных звезд, которые, после быстрой термоядерной эволюции, порождают черные дыры. Объекты, образовавшиеся в результате слияний, обычно имеют высокую пространственную скорость ("убегающие звезды"). Важные детали данных процессов были проверены методом N-тел.

В небольших скоплениях число сливающихся объектов ограничивается просто количеством массивных звезд, в больших скоплениях - числом массивных звезд в их ядрах.

Многие классические статьи, особенно опубликованные не в тройке ведущих журналов, достаточно малоизвестны и малоцитируемы просто потому, что они не доступны в Сети. Приятно, что некоторые из классиков выкладывают свои старые работы в Сеть, да еще и прямо в Архив.

Как ясно из названия, в статье рассмотрена эволюция плотных звездных скоплений. За счет взаимодействия звезд друг с другом часть из них выбрасывается из скопления. Оставшиеся образуют все более и более плотное скопление. В конце концов скопление коллапсирует.

Это обзор по динамике планетных систем в применении к экзопланетам. Статья достаточно техническая, но вместе с тем доступная каждому, кто помнит стандартный университетский (институтский) курс по теормеху.

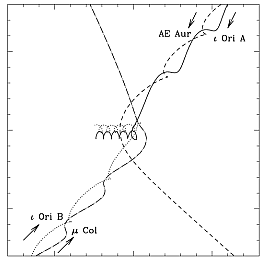
От туманности Ориона в почти противоположных направлениях удаляются две одиночные убегающие звезды AE Aurigae и μ Columbae. Кроме того от туманности со скоростью большей 100 км/с летит двойная система ι Ori с эксцентриситетом орбиты e=0.8. Все эти звезды вылетели из туманности примерно 2.5 млн. лет назад. Авторы работы пытаются смоделировать данное событие.

Схема одного из вариантов разлета

Очень объемная статья, посвященная численному исследованию устойчивости существующих планетных систем. Планетными системами обладают звезды, у которых открыто уже хотя бы две планеты. Таких систем известно около десяти, авторы провели моделирования для ипсилон And, HD83443, GJ876, HD82943, 47UMa, HD168443 и, конечно, для Солнечной системы.

Моделирование заключалось в следующем: для каждой системы 1000 раз проводилось численное интегрирование ее движения на интервале примерно в 1 миллион лет. Параметры систем брались из наблюдений и слегка варьировались.

Выводы авторов таковы: резонансные системы (HD82943 and GJ876) имеют очень узкую область устойчивости; взаимодействующие (но без резонанса) системы (ипсилон And, 47UMa и Солнечная система) - гораздо более широкую область стабильности; а широкие системы (таких много, авторы провели моделирование только для HD83443 и HD168443) устойчивы.

^{(Архив Динамика:} v.2, 2003, v.1, 2002-2003)